Many people have an aversion to Mathematics. There are lots reasons for this, some of which I have talked about before, but we won’t get into that. Today I would like to discuss something that I think could change how Mathematics is taught and learned: dynamic and/or interactive representations. It is easiest to start off with an example so here ya’ go, example 1:

This animation is… awesome to say the least. Seriously, I love it! It shows the viewer exactly what is meant by a radian. All it is is the measure of a circle’s radius along its circumference. Simple as that. For students this is sometimes something that is lost in translation when they start their trig classes. Degrees of a circle are ingrained so deeply that it is hard for them to shed that notion and jump to the more natural radians. Fig. 1 helps in actually seeing what is meant my a radian. This is a huge teaching tool. There are many people who learn by seeing and being able to visualize mathematical formulas/equations is essential to their learning pattern. Even those who do not learn by visualizations can benefit from this animation since it provides a different perspective on how to ‘see’ the concept. I love this particular animation because it is so simple.
How about another more complex animation? Example 2:
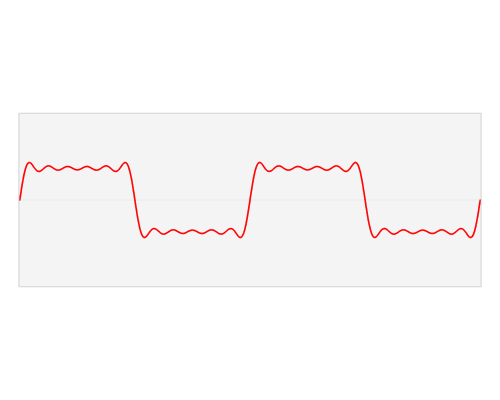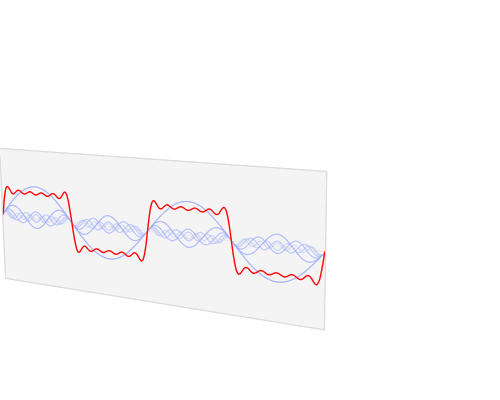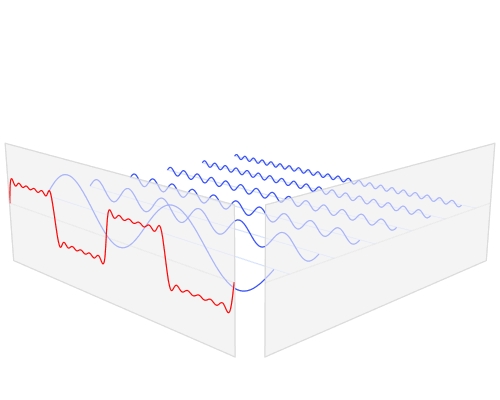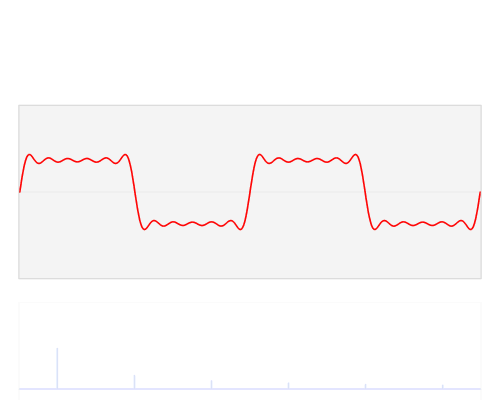
If you have ever had any trouble grasping parts of Fourier Analysis (which most people have) then this animation is for you. It is so super simple but also so enlightening! I love watching it. I remember struggling when I first learned the Fourier Transform (FT) to understand exactly what it meant to go from time to frequency domain. The concepts were there but what I was missing was a picture to tie it all together. I would have loved to see this animation when I first learned FTs, it would have helped out a lot.
And for the continuous case of Fig. 2:
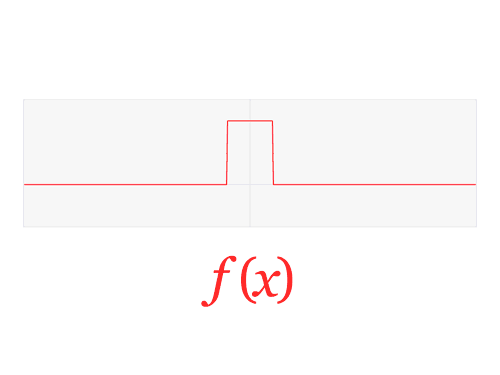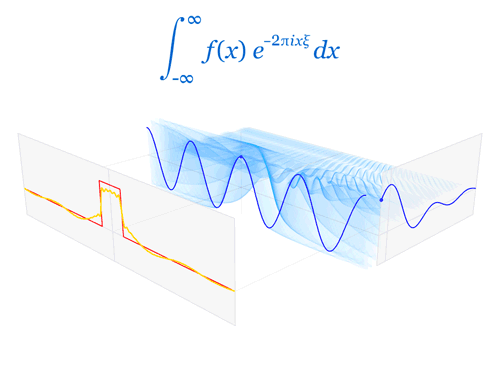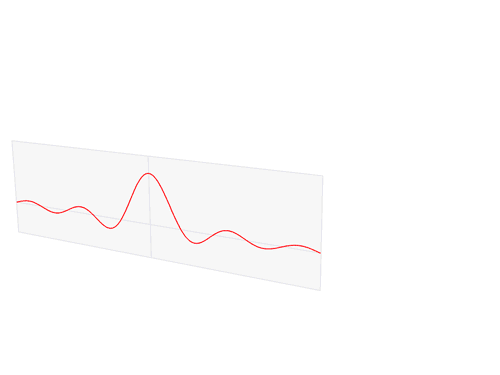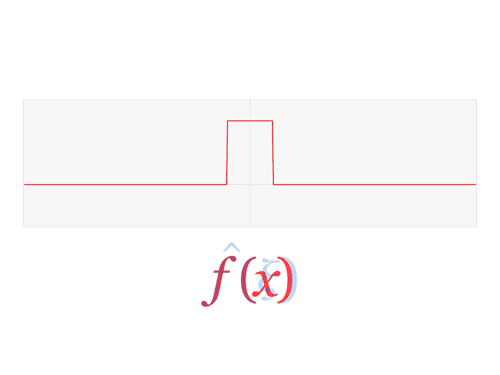
This one is even cooler than Fig. 2 to me since I have used it so much in all my endeavors in Quantum Computing. You can’t go an inch in Quantum Mechanics without having to jump between time and frequency domains, it makes calculations so much easier to work in one rather the other. Lots of symmetries can be exploited in different domains (same concept as coordinate transforms that yield symmetries that were previously not visible).
Amazingly, all of these animations were created by one guy! He does a great job at creating mathematical and physical animations so check out his work!
And just to blow your socks off, take a look at this live demonstration of the Pythagorean Theorem:
Seriously, wasn’t that awesome?! I have had countless students ask me during tutoring/recitations/teaching that wanted clarifications on why the Pythagorean Theorem ‘works’ and what it means. This video shows exactly what it means and puts it better than I ever could in words. I’m not exactly sure why I find it so mind blowing but I do. I think it is one of the most awesome representations of a mathematical equation I have ever seen in my entire life.
Animations and physical representations of mathematical constructs are amazing. They can sometimes provide insights and understandings into Mathematics that the equations just can’t obtain on their own. Not everyone can look at an equation and understand its true meaning right away. I would argue that most people are not able to do this. These animations make it easy to ‘see’ what is meant by an equation.</p>
Now that we have seen and talked about mathematical animations, I would like to briefly discuss interactive learning. Interactive learning is a natural extension of animations. What would make an animation better? Give control over variables in the animation to the viewer, of course! The best example I can think of is using something like Mathematica and the Animate (or Manipulate) command. This produces an interactive plot (or whatever you created) so that the viewer can manipulate certain properties of the figure. Many new online textbooks are going this route so that students will be able to interact with the book to better understand concepts. This is an invaluable tool for the future and will be a game changer in the education world, especially since everyone now has a smart phone/laptop that they are carrying around. This already allows them to have instant access to the internet so having an interactive learning tool along with that could really make a difference in how students learn in the future.
I think I'm going to follow-up soon with a post that uses Mathematica's CDF viewer to showcase how an interactive textbook works and some of the neat things that they can do. However, you have to have the plugin installed to view the CDF file so I have to go download that before I can make one!

